Visão Geral
Neste primeiro capitulo vamos falar sobre as vantagens da linguagem Assembly, as funções básicas do Hardware, sistemas numéricos, aritmética binária e por fim de endereçamento.
Vantagens da linguagem Assembly
O entendimento da linguagem assembly fornece o conhecimento de:
- Interfaces entre o programa e o SO (Sistema Operativo), processador e BIOS;
- Representação dos dados em memória e em outros dispositivos externos;
- Como o processador acede e executa instruções;
- Como instruções acedem e processão os dados;
- Como o programa acede a dispositivos externos.
Outras vantagens do usar a linguagem Assembly são:
- Requer menos memória e tempo de execução.
- Permite executar um trabalho complexo a nível de hardware de uma forma fácil.
- É ideal para trabalhos que requerem o menor tempo possível.
- É extremamente util para a escrita de serviços de interrupções ou outras programas residentes em memória.
Funções básicas do Hardware
Os principais componentes de um PC são o processador, memória e os registers (registos). Os registers são componentes do processador que guardam dados e endereços. Para executar um programa, o sistema copia-o do dispositivo externo para a memória interna. O processador executa instrução a instrução do programa.
A unidade fundamental de armazenamento é o bit, este pode ser ligado (1) ou desligado (0). Um grupo de nove bits relacionados fazem um byte. Os primeiro oito bits são usados para dados e o nono bit é usado para paridade, como uma forma de detecção de erros. De acordo com as regras da paridade, o numero de bits que são 1's em cada byte deve ser sempre par.
Então, a paridade é usada para fazer o numero de bits num byte par. Se a a paridade for impar, o sistema assume que houve um erro de paridade (extremamente raro), que pode ser causado por falhas no hardware ou uma interferência elétrica.
Os processadores suportam os seguintes tamanhos de dados:
Word: um dado composto por 2 bytesDoubleword: um dado composto por 4 bytes (32 bits)Quadword: um dado composto por 8 bytes (64 bits)Paragraph: um dado composto por 16 bytes (128) bitsKilobyte: 1024 bitsMegabyte: 1 048 576 bytes
Sistema de numeração binário
Cada posição é uma potência de base 2 que começa em 0 e é aumentada em 1.
A tabela a baixo mostra o valor da posição de um numero de 8-bit, e cada bit está definido para 1.
| Valor do Bit | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
|---|---|---|---|---|---|---|---|---|
| Valor da posição | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| Numero do Bit | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
O valor do numero em binário e dado com base nos 1's e no seu valor posicional. Então, o valor para o numero binário a cima é: 1 + 2 + 4 + 8 + 16 + 64 + 128 = 255, que é o mesmo que 2^8 - 1.
Sistema numérico hexadecimal
O sistema hexadecimal usa uma base 16. Os valores vão de 0 até 15. Por convenção, as letras de A até F é usada para representar os dígitos correspondentes aos valores de decimal 10 até 15.
O uso principal do sistema hexadecimal na computação é essencialmente para abreviar a comprimento da representação do binário. Basicamente, o sistema numérico hexadecimal representa os dados em binário dividindo cada byte ao meio e expressão o valor de cada meio byte. A tabela a baixo fornece uma representação do equivalente em decimal, binário e hexadecimal.
| Decimal | Binario | Hexadecimal |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 2 | 10 | 2 |
| 3 | 11 | 3 |
| 4 | 100 | 4 |
| 5 | 101 | 5 |
| 6 | 110 | 6 |
| 7 | 111 | 7 |
| 8 | 1000 | 8 |
| 9 | 1001 | 9 |
| 10 | 1010 | A |
| 11 | 1011 | B |
| 12 | 1100 | C |
| 13 | 1101 | D |
| 14 | 1110 | E |
| 15 | 1111 | F |
Para converter de binário para hexadecimal, divide-se o numero em grupos de 4, começando a direita para a esquerda, e escreve-se esses grupos no seu correspondente em hexadecimal.
Exemplo: Numero binario 1000 1100 1101 0001 é equivalente a 8CD1.
Para converter de hexadecimal para binário, basta escrever cada numero num grupo de 4 dígitos do seu correspondente em binário.
Exemplo: O numero hexadecimal FAD8 é equivalente ao binário 111 1010 1101 1000.
Aritmética binária
A tabela a baixo mostra quatro simples regras na adição binária:
| (II) | (II) | (III) | IV |
|---|---|---|---|
| 1 | |||
| 0 | 1 | 1 | 1 |
| +0 | +0 | +1 | +1 |
| =0 | =1 | =10 | =11 |
A regra (III) e (IV) mostram um transporte de 1-bit na próxima posição à esquerda.
Exemplo
| Decimal | Binario |
|---|---|
| 60 | 00111100 |
| +42 | 00101010 |
| =102 | 01100110 |
A forma como se representa um numero negativo em binário é expresso em uma notação de complementos de dois. De acordo com esta regra, para converter um numero binário para o seu negativo tem que reverter a ordem dos bits e adicionar 1.
Exemplo
| Numero 53 | 00110101 |
| Reverter | 11001010 |
| Adicionar 1 | 1 |
| Numero -53 | 11001011 |
Para subtrair um valor a outro, convertemos o numero que vai ser subtraído para um formato de complementos de dois e adicionamos os números.
Exemplo: Subtrair 42 a 53
| Numero 53 | 00110101 |
| Numero 42 | 00101010 |
| Reverter o 42 | 11010101 |
| Adicionar 1 | 1 |
| Numero -42 | 11010110 |
| 53 - 42 = 11 | 00001011 |
O excesso do ultimo bit 1 é perdido.
Endereçamento de dados na memoria
O processo que através do processador controla a execução das instruções é referente ao ciclo fetch-decode-execute (procurar-descodificar-executar) ou ciclo de execução. Este consistem em três etapas continuas:
- Procurar pela instrução em memória
- Descodificar ou identificar a instrução
- Executar a instrução
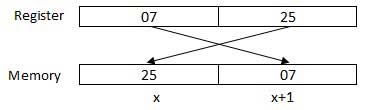
O processador deve aceder a um ou mais bytes de memória de cada vez. Vamos considerar o numero hexadecimal 0725H. Este numero vai necessitar de dois bytes de memória. O bytes de maior ordem ou o byte mais significativo é 07 e o de menor ordem é o 25.
O processador guarda os dados na ordem reversa dos bytes, como por exemplo, os bytes de menor ordem são guardados em endereços de memória mais baixos e os bytes de maior ordem em endereços de memória mais altos. Então, se o processador precisar de trazer o valor 0725H do registo para a memória, isto vai transferir o 25 para o endereço mais baixo e o 07 para o endereço seguinte de memória.
x: endereço de memoria
Quando um processador obtém os dados numéricos da memória para o registo, ele reverto novamente os bytes. Existem dois tipos de endereços de memória:
Endereço absoluto: Referencia direta para uma localização especifica.Endereço do segmento (ou offset): Endereço inicial de um segmento de memória com o valor de deslocamento.